Optimizing ROP through automation

Algorithm interprets drilling mechanics data to automatically control drilling parameters

By Jonathan Dunlop, Rustam Isangulov, Walt Aldred, Hector Arismendi Sanchez, Jose Luis Sanchez Flores, Jose Alarcon Herdoiza, Jim Belaskie, J.C. Luppens, Schlumberger

Increasing the rate of penetration without detrimentally affecting hole quality or well placement can help to reduce drilling costs, especially on rigs with a high spread rate. This article discusses a rate-of-penetration (ROP) optimization algorithm for polycrystalline diamond compact (PDC) bits. The algorithm does not support roller-cone bits or underreamers, but the method could apply to them.

While on bottom, the driller can control only three parameters: weight on bit (WOB), rotary speed and mud flow rate. Without a mud motor in the drill string, flow rate has a limited effect on ROP, so the optimization is two dimensional in WOB and revolutions/min (RPM).

PDC bit model

The drilling response of a PDC bit is modeled as three distinct operating phases, each with a linear relationship among WOB, bit torque, and depth of cut per revolution.

Phase I: At low WOB, most interaction between the bit and rock occurs at the cutters’ wear flats. Neither the rock surface nor the wear flat will be perfectly smooth. As depth of cut increases, the rock beneath the contact area will fail, and the contact area will enlarge. This continues until a critical depth of cut is reached. At that depth, the failed rock fully conforms to the geometry of the wear flats, and the contact area no longer grows.

Phase II: Beyond the critical depth of cut, any WOB increase translates into cutting. The bit incrementally behaves as a sharp bit until the founder point is reached, when cuttings are produced at a rate that can’t be efficiently cleaned by mud flow; they get trapped between the bit matrix and the uncut rock and begin to support some of the WOB.

Phase III: The response past the founder point depends on how quickly the excess WOB is applied. When rapidly applied, the trapped cuttings will undergo further plastic deformation, and the bit incrementally behaves similarly to Phase I. Depth of cut will slightly increase with increasing WOB, generating more cuttings. This is unsustainable and will quickly converge to the same response as if the WOB had been slowly applied. The mud flow path will be smaller than it was at the founder point because of the trapped cuttings, so the steady-state cuttings production rate must be lower than what it was at the founder point.

Cuttings production rate is proportional to depth of cut; therefore, the depth of cut must decrease after the founder point is reached.

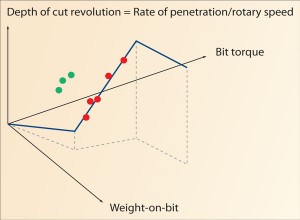
Depth of cut per revolution can be estimated by dividing ROP by RPM. Real-time drilling data can be plotted in the 3D WOB, bit torque and depth of cut space. As the bit drills into a new formation, the response will abruptly change and the points will fall on a new line (Figure 1).

A straight line in three dimensions has four unknown parameters: two slopes and the intersection with the x–y plane (in this case, the WOB–torque plane). These parameters could be estimated with a least-squares fit to a temporal or spatial sliding window (e.g., last five minutes or last 10 ft of data), but this would provide poor fits in the vicinity of formation boundaries.

For example, in Figure 1, plotting a straight line through both the red and green points would yield bizarre model parameters. These models have been successfully applied in the field by manual inspection of the data and separating the points into homogeneous segments. In Figure 1, a straight line would fit the red data points, and a second straight line would fit the green points, thereby avoiding the cross-class polluted estimates produced by a moving window.

This is a labor-intensive process that has prevented the field from routinely applying these models in the 25 years since their development.

Changepoint detection

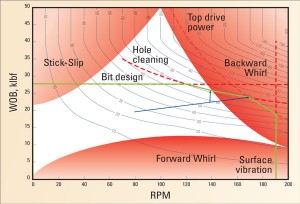
Changepoint detectors are algorithms that divide a heterogeneous data series into a sequence of homogeneous segments to automate the previously described process. A Bayesian changepoint detector that processes streaming data provides the segmentation, and the parameters of the most recent segment are used to predict the bit response to possible changes in the values of WOB and RPM. Projecting the three-dimensional fit onto the WOB–depth-of-cut plane gives a linear equation linking WOB, RPM and ROP. This can be rearranged to give ROP as a function of WOB and RPM (Figure 2).

The coefficients of the bit/rock model allow various constraints to the drilling process to be expressed as a function of WOB and RPM:

• ROP at which cuttings are being generated too fast to be cleaned from the annulus;

• WOB that will generate excessive torque for the top drive;

• WOB that will generate excessive torque for the drill pipe; and

• RPM that causes excessive vibration of the derrick.

The region below these constraints is the safe operating envelope. The WOB and RPM that generate the maximum ROP within the safe operating envelope may be sought and communicated to the driller. Alternatively, the WOB and RPM may automatically pass to an autodriller. This approach may push the system into regions where drill string vibration will occur. These may be identified by signatures in surface measurements or by downhole shock measurements, if available. The user may then pull back to a region of stable drilling and use the display to optimize the ROP in a more supervised mode of operation.

If a suitably robust vibration model were developed, it could be incorporated as another constraint, but these models are very sensitive to unknown boundary conditions of the borehole. Their use for prediction is, so far, limited.

Data preprocessing

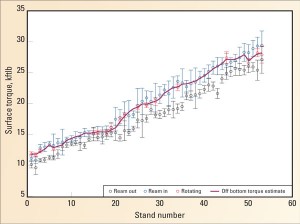
Torque is measured on the surface, but bit torque may be significantly lower because of the drill string touching the borehole wall. When the bit is off bottom and rotating, the bit torque should be zero, so the observed surface torque should all be due to the frictional losses. These observations are plotted in red in Figure 3.

At the end of drilling a stand, drillers often work the pipe to help flush cuttings up the hole; the surface torque during these upward and downward movements are shown in black and blue, respectively, in Figure 3. The red points are generally much closer to the blue points than the black. For some stands when the driller does not rotate off bottom, the reaming-in point is substituted as an observation of off-bottom torque.

A Kalman filter estimating the off-bottom torque is shown in magenta in Figure 3. Bit torque is then estimated as surface torque minus off-bottom torque.

Using the same approach, another Kalman filter estimates off-bottom hookload; WOB is then estimated by off-bottom hookload minus hookload.

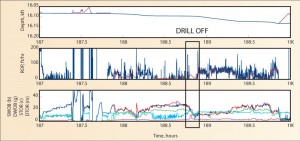
While on bottom, drillers apply WOB by moving the pipe downward a few inches, holding it steady while the WOB “drills off” as the pipe stretches, then apply WOB again. Conventional estimates of ROP compute the average more than a 1 ft- or 5 ft-spatial window and give a constant value during each drill-off, whereas in reality the ROP downhole reduces as the WOB reduces. This error would corrupt the depth-of-cut estimate and inject noise into the bit/rock model. A compliance-corrected ROP model is employed to model the elastic response of the drill string and produce a much more realistic ROP during each drill off (Figure 4).

Constraint models 

A top drive generally produces less torque at higher RPM; the optimizer must be aware of this to model the top drive with piecewise linear and cubic splines.

Rig contractors generally operate at around 80% of the output, so a derating coefficient is included in the setup. The upper envelope of the bit torque versus WOB relationship is obtained by taking the regression in Figure 1 and adding three times the estimate of the standard deviation of the torque noise. Also adding the off-bottom torque estimate gives the relationship between the upper envelope of surface torque and WOB. This can be used to remap the surface torque axis of the top-drive output curve into WOB to give a constraint in the RPM–WOB plane that is valid for that particular instant.

Given the dimensions of the drill string and borehole, the trajectory and mud rheological properties, a hydraulics module outputs a graph of ROP versus the mud flow rate that would clean the hole at that steady-state ROP. The driller picks a flow rate that allows the annular pressure to be kept inside safe limits.

This gives the maximum ROP at which the hole can be efficiently cleaned. If this ROP were used directly as a constraint, there would not be a unique solution to the optimization, so a tapered 1 ft/hr advantage is applied at 120 RPM in an ad hoc manner.

Field test examples 

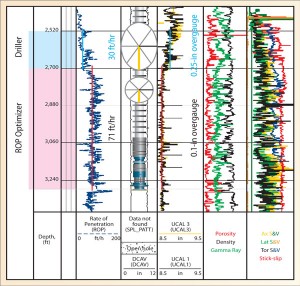
Figure 5 shows an early field experiment of the algorithm where downhole WOB, downhole torque, azimuthal ultrasound caliper log and various shock and vibration measurements were taken.

The driller made a hole as fast as possible for two stands, then took recommendations from the algorithm for the next seven stands. Figure 5 shows that the lithologies were comparable and that similar levels of shocks were seen in both cases. ROP increased by a factor of 2.4, from 30 ft/hr to 71 ft/hr. Hole overgauge decreased by a similar factor of 2.5, from an elliptical 0.25 in. to a circular 0.1 in. overgauge. Minimizing overgauge is advantageous for tripping the pipe and running casing without getting stuck, cementing the casing and steering a directional well.

The algorithm has drilled in excess of 35,000 ft of hole across all field tests. It has been tested in hole sizes ranging from 6 ¾ in. to 16 in. and at all inclinations from vertical to horizontal. The resulting ROP from each test was compared with either the driller’s performance in the same hole section with comparable lithology or the field average with a comparable bottomhole assembly. The average ROP gain was 32%.

During the experiment in November 2008 (Figure 5), the driller was accountable for not letting the algorithm damage the rig, whereas the other drillers had the extra accountability for delivering a well that could be successfully cased; this led to the reluctance of some drillers to fully apply the recommendations.

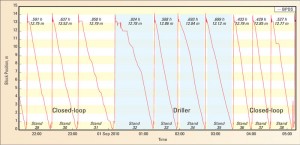
The driller was applying considerably lower RPM than the algorithm recommended, and because of the 50% step size, the optimal RPM that the algorithm wanted the driller to eventually reach was higher still. The field-test coordinator eventually increased the step size to 90% to lure the driller further out of his comfort zone.

Complex social issues such as these can be modified or avoided by feeding the recommended WOB and RPM directly to the controls of the drilling rig.

Conclusions

Automated interpretation of drilling mechanics data can be used to control drilling parameters and to improve performance, consistency and hole quality. Automation will not replace drillers but should help them deal with the more mundane and repetitive tasks so drillers can concentrate on the safety of the rig crew and wellbore. The algorithm does not currently use any offset well data so set-up time is minimal. Future versions of the algorithm may include offset well analysis, as this would allow inclusion of:

• An estimate of the abrasivity of upcoming formations and a bit-wear model to project the expected bit wear to the next casing point;

• An algorithm to drill off the WOB before encountering a known stringer or other formation that may damage cutters; and

• An algorithm to suggest an alternative bit or rig equipment upgrade.

This article is based on IADC/SPE 139897, “Increased Rate of Penetration Through Automation,” presented at the 2011 SPE/IADC Drilling Conference & Exhibition, Amsterdam, 1-3 March 2011.

References:
1. Aldred, W.D., Dunlop, J. and Belaskie, J., System and Method for Online Automation, 2010 International Patent Application PCT/IB2009/007127, Publication number WO 2010/043951 A2.
2. Detournay, E., Method of Determining the Drilling Conditions Associated with the Drilling of a Formation with a Drag Bit, 1993 US Patent No. 728,442.
3. Detournay, E., Richard, T., and Sheppard M.,  “Drilling Response of Drag Bits: Theory and Experiment,” 2008 International Journal of Rock Mechanics & Mining Sciences 45: 1347–1360.
4. Mims, M.G., Krepp, A.N., and Williams, H.A., Drilling Design and Implementation for Extended Reach and Complex Wells, Second Edition, 1999, Houston: K&M Technology Group.